轉子流量計的流量與密度的關系
點擊次數:9103 發(fā)布時間:2020-08-19 06:51:03
流量計的基本原理是依據浮子兩側的壓差形成向上的推力
即

式中
p1和p2---上、下游流體的壓力;
K---壓力損耗系數;
ρ---流體的密度;
v---流體通過環(huán)形通大道的流速。
若以體積流量qv替代流速v,即
v=qv/Aring
式中
Aring--浮子周圍的環(huán)形面積。
由次則可得出
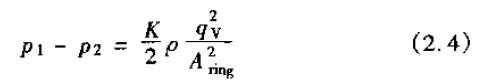
在式(2.4)中假設在入口處動力源的影響忽略不計,且浮子兩側的差壓是由浮子下游動力源的損耗所造成的,那么,浮子的浮子為
W=VR(ρs-ρ)g
式中
Vs---浮子的體積;
ρs---浮子材料的比重;
g---重力加速度。
由于浮力W=As(p1-p2),式(2.5)可寫成
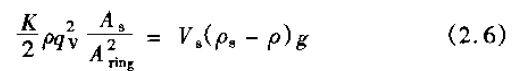
式中 As---浮子的*大截面積。
式(2.6)經整理得到
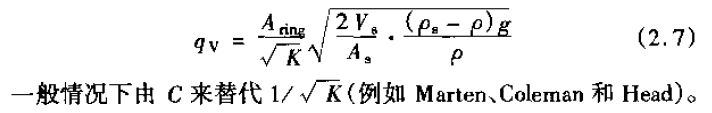
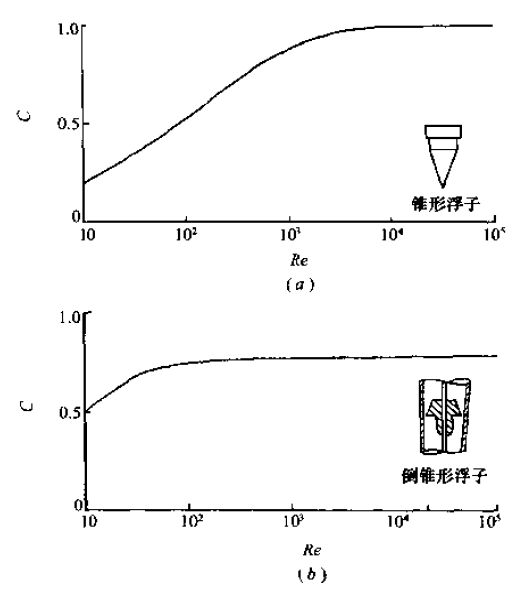
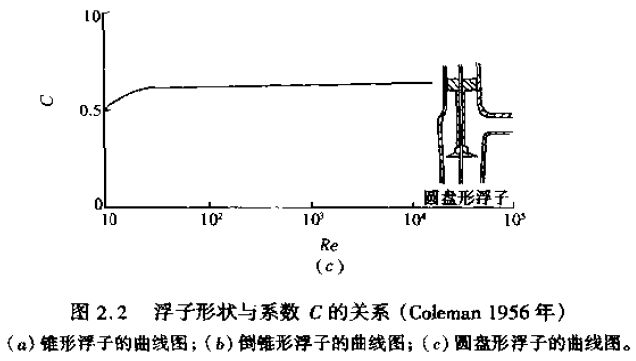
Coleman(1956年)曾對3種不同形狀的浮子給出了C值,如圖2.2所示,并提出,在*大流量時,C值的取值范圍為從0.6(低雷諾系數敏感的浮子)到接近于1。
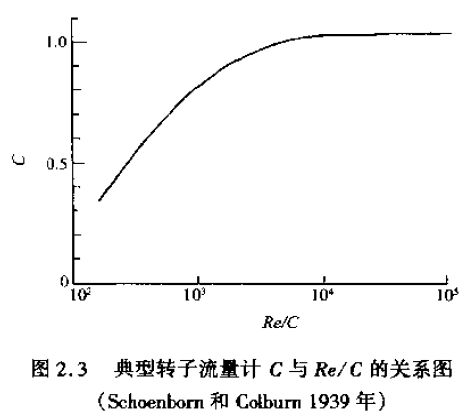
圖2.2顯示,在小流量時C值有所下降,這也反映了這樣一個事實,即隨著雷諾系數的下降,使通過一個開口的損耗系數增加(Millerl990)。在Coleman的圖中可以看出各種不同的浮子形狀對枯度的影響,圖2.2的實質是雷諾系數對錐形浮子的C值影響*Schoenborn和Colburn(1939年)給出了C與Re/C的關系曲線圖,
其中Re是以Deq為基準的雷諾系數。Deq稱為等效直徑,其定義為D與d的差值,如圖2.3所示。當時,他們設計了一臺人型高壓裝置,用一根鋼管加上一支伸出的小棒作為指針,在一個帶有刻度的玻璃窗口中運動。圖2.3的曲線是在這臺設備上得出的一條*佳曲線。由于考慮到浮子兩側壓差產生的上升力作用,他們在實驗中施加了一個能平衡液體中浮子重量的作用力。他們還注意到,在大型儀器中此曲線對流體自身的影響比小型儀器要小。


其中Re是以Deq為基準的雷諾系數。Deq稱為等效直徑,其定義為D與d的差值,如圖2.3所示。當時,他們設計了一臺人型高壓裝置,用一根鋼管加上一支伸出的小棒作為指針,在一個帶有刻度的玻璃窗口中運動。圖2.3的曲線是在這臺設備上得出的一條*佳曲線。由于考慮到浮子兩側壓差產生的上升力作用,他們在實驗中施加了一個能平衡液體中浮子重量的作用力。他們還注意到,在大型儀器中此曲線對流體自身的影響比小型儀器要小。
雖然對轉子流量計的定量很困難,但在同樣讀數基礎上能夠把一種流體的流量值換算成另一種流體的流量值。Schoenborn和Colburn(1939年)給出了與ISA(1961b)很近似的計算公式
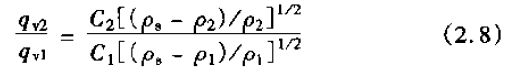
其區(qū)別在于1SA(1951b)所給的公式中省略了C2/C1,這里可認為其比值為1。Coleman(1956年)利用此公式時也把C2/C1看做1,即認為粘度的變化可忽略不計。他指出這樣一個事實,假如式(2.7)的體積流量改寫成質量流量,即
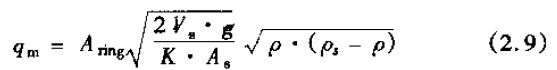
對流體密度的變化求導
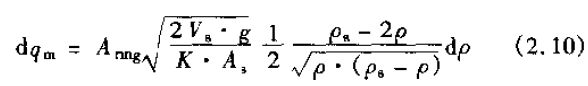
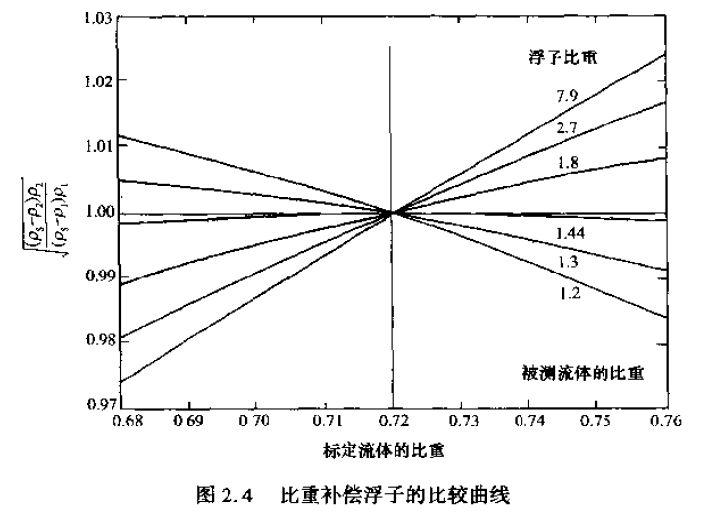
即可得出一個結論:對一個比重2倍于介質的浮子,質量流量變化為0。也就是說,它對密度變化的敏感*小(參見Head 1964年)。根據對比重為0.72的航空汽油標定的結果,圖2.4表示了當流體密度變化時和在各種不同浮子情況下的密度修正系數。Head(1964年)認為,設計一種氣流向下的裝置,設浮子的比重為0,對它的體積流量方程進行微分運算,可以獲得某些可能的進展。Head還提出,浮子的自動補償可允許溫度其他參數的變化。
上一篇:關于串接式超聲波流量計基本概述
下一篇:渦街流量計的特性有哪些














